# 环境安装

# 第一步下载虚拟机

https://www.vmware.com/

虚拟机官网

# 第二步下载镜像

https://releases.ubuntu.com/20.04.4/ubuntu-20.04.4-desktop-amd64.iso?_ga=2.90337498.1753593614.1646563933-382193276.1643206315

下载链接，如果不能用或者想安装其它版本的，就删掉后面的去官网找。

# 第三部配置镜像文件

创建新的虚拟机时将镜像文件导入即可

# 第四步更新 gcc

sudo apt install build-essential gcc-multilib g++-multilib

输入即可

# 解题

# 1. bitXor

题目要求用“与”和“非”表达异或，

先找异或表达式 a ^ b=(~ a & b) | ( a & ~ b )，发现只要将 “或” 替换成 “与” 和 “非” 的表达式即可，有因为 “与” 和 “或” 完全相反，得 a & b = ~ （ ~ a | ~ b ）；a | b = ~ （ ~ a & ~ b ）。因此 a ^ b = ~ ( ~ ( ~ a & b ) & ~ ( a & ~ b ));

	int bitXor(int x, int y) {
	return ~(~(~x&y)&~(x&~y));
	}

# 2. tmin

要求返回2进制的最小值，

即：0x80000000。允许使用位移符直接将 1 移到第 32 位即可。1<<31.

	int tmin(void) {
	int a = 3;
	return a << 31;
	}

# 3.isTmax

判断x是不是最大值

最大值加一等于二进制最小值：80000000，80000000 加它（800000000）取反为 ffffffff，再取反为全 0，！后即为 true，但如果这个数是 ffffffff，那么它加一后（00000000）取反加它（00000000）本身也是 ffffffff，再取反为全 0，！后也为 true。根据下图第一次运算到 E 后从下面的 C 接着运算排除 ffffffff。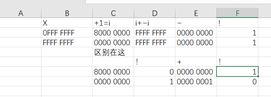
在这里插入图片描述

	int isTmax(int x) {
	int i = x+1;
	x = x + i;
	x = ~x;
	x=(x+!i);
	return !x;
	}

# 4. allOddBits

判断奇数为上是否全为一

先给出一个全一的数，和 x 先与后异或，如果 x 和给定的数在奇数位上相同，则结果将为零。
左后用！判断

	int allOddBits(int x) {
	int a = 0xAA + (0xAA<<8);
	a = a + (a<<16);// 令 a=AAAAAAAA
	return !((x&a)^a);// 如果位置上有不是一的，那么括号内的结果不为零，！后返回 0；
	}

# 5. negate

求相反

根据～a = - （ a + 1 ）得：- x = ~ x + 1.

	int negate(int x) {
	return ~x+1;
	}

# 6. isAsciiDigit

判断x是否是大于0x30，小于0x39的数

用减法作答，主要用符号位进行判断

	int isAsciiDigit(int x) {
	int a=0x2f+(~x+1);
	int b=0x39+(~x+1);
	a=a>>31;// 如果符合要求则 a 现在为 0x1，使用 0x2f 是防止将 0x30 排除掉。
	b=b>>31;// 如果符合要求则 b 现在为 0，这时使用 0x39 是因为不影响答案。
	b=!!a&(!b);
	return b;
	}

# 7.conditional

进行x ? y : z运算

利用 x 的布尔值进行取舍

	int conditional(int x, int y, int z) {
	int a=!!x;
	int b=~a+1;// 如果 x 为零则此时 b 为零，如果 x 不为零则 b 为全一
	int c=~(~b&y)+1;// 如果 b 为零则 c 为 y 的相反数，否则为 0x80000000
	int d=~(b&z)+1;// 如果 b 为 1 则 c 为 y 的相反数，否则为 0x80000000
	return y+z+c+d;
	}

# 8.isLessOrEqual

判断xy的大小

判断大小 >> 使用布尔值

	int isLessOrEqual(int x, int y) {
	int a=!((y+~x+1)>>31);//y 大时 a 为 1，x 大时 a 为 0
	int b=(x>>31)^(y>>31);// 判断是否是一负一正，是 >>1
	int c=b&(x>>31);// 判断 x 是否为负数，是 >>1
	return !!c\|(!b)&a;
	}

# 9.logicalNeg

实现逻辑非

利用相反数是除 0 之外的都为一正一负，然后位移 31 位即可，有个特例 0x80000000，它取相反数还是它本身因此在返回时将 x 和它的相反数在进行一次取反，这是 0x80000000 的符号位都为 0，且对判断没有影响

	int logicalNeg(int x) {
	int y=~x+1;// 取 x 的相反数
	return ((~y&~x)>>31)&1;
	}

# 10.howManyBits

计算x补码所需的最小位数

如果是一个正数，则需要找到它最高的一位（假设是 n）是 1 的，再加上符号位，结果为 n+1；如果是一个负数，则需要知道其最高的一位是 0 的（例如 4 位的 1101 和三位的 101 补码表示的是一个值：-3，最少需要 3 位来表示）。
计算 n 则使用二分法进行。

	int howManyBits(int x) {
	int a0,a1,a2,a4,a8,a16;
	int w;
	int sign=x>>31;
	x = (sign&~x)\|(~sign&x);
	a16=(!!(x>>16))<<4;// 如果高 16 位不为 0, 则我们让 b16=16
	x=x>>a16;// 此处是否位移取决于高 16 位是否有数字
	a8=(!!(x>>8))<<3;
	x=x>>a8;
	a4=(!!(x>>4))<<2;
	x=x>>a4;
	a2=(!!(x>>2))<<1;
	x=x>>a2;
	a1=(!!(x>>1));
	x=x>>a1;
	a0=x;// 判断最后一位是否为一
	w=1+a16+a8+a4+a2+a1+a0;
	return w;
	}

# 11.floatScale2

求一个浮点数的erbei

浮点型公式 x=(-1)^(1.frac) 的 exp 次方。
如果 exp=255 并且尾数非 0 就是 NaN 直接 return 就好其次如果 frac 全为 0 那么则表示无穷大这两种情况都可以直接 return
如果 exp=0 则表示非规格化数那么直接返回 uf*2 即 frac>>1。
剩余的即为规格化数，此时将 exp+1 即可。

	unsigned floatScale2(unsigned uf) {
	unsigned exp = (uf&0x7f800000)>>23;// 指数
	unsigned sign=uf>>31&0x1;// 符号数
	unsigned frac=uf&0x7FFFFF;// 尾数
	unsigned res;
	if(exp==0xFF) return uf;
	else if(exp==0){
	frac <<= 1;
	res = (sign << 31) \| (exp << 23) \| frac;
	}
	else{
	exp++;
	res = (sign << 31) \| (exp << 23) \| frac;
	}
	return res;
	}

# 12.floatFloat2Int

将浮点型整形化（c语言中使用强制转换）

如果是小数 E< 0 的情况我们直接返回 0
如果是 exp=255 的情况直接返回 0x80000000u
这里注意如果超范围了也会直返回 0x80000000u
因此可以直接用 E>=31（这里如果大于 31 则超出了整形能表是的范围）来判断
如果是规格化数则我们进行正常处理
先给尾数补充上省略的 1 判断 E<23 则尾数需要舍去 23-E 位根据符号位返回就好

	int floatFloat2Int(unsigned uf) {
	unsigned exp = (uf&0x7f800000)>>23;
	int sign=uf>>31&0x1;
	unsigned frac=uf&0x7FFFFF;
	int E=exp-127;
	if(E<0)return 0;// 为零
	else if(E >= 31){
	return 0x80000000u;
	}// 超限
	else{
	frac=frac\|1<<23;// 在前面补上 1
	if(E<23) {// 此时判断 e 是否大于 23，因为此时 frac 相当于已经被 & lt;<23 了，此步骤为了缺认位移的数量是否正确
	frac>>=(23-E);
	}else{
	frac <<= (E - 23);
	}
	}
	if (sign)
	return -frac;
	else
	return frac;
	}

# 13.floatPower2

求2的x次方，返回值为浮点数

因为求 2 的次方，因此尾数为零，首先得到偏移之后的指数值 e，如果 e 小于等于 0（为 0 时，结果为 0），对应的如果 e 大于等于 255 则为无穷大或越界了。否则返回正常浮点值，frac 为 0，直接对应指数即可。

	unsigned floatPower2(int x) {
	int e=x+127;
	if(e<=0) return 0;
	if(e>=255) return 0xff<<23;
	return e<<23;
	}